Srinivasa Ramanujan

Birth

Srinivasa Ramanujan, an Indian mathematician was born in 22nd December, 1887 in Madras, India. Like Sophie Germain, he received no formal education in mathematics but made important contributions to advancement of mathematics. His acquaintance G.H. Hardy summed up his achievement in following words:

“The limitations of his knowledge were as startling as its profundity. Here was a man who could work out modular equations and theorems…to orders unheard of, whose mastery of continued fraction was… beyond that of any mathematician in the world, who had found for himself the functional equation of zeta function and the dominant terms of many of the most famous problems in analytical theory of numbers; and yet he had never heard of a doubly periodic function or of Cauchy’s theorem, and had indeed but the vaguest idea of what a function of complex variable was…”

Contribution to Mathematics

His chief contribution in mathematics lies mainly in analysis, game theory and infinite series. He made in depth analysis in order to solve various mathematical problems by bringing to light new and novel ideas that gave impetus to progress of game theory. Such was his mathematical genius that he discovered his own theorems. It was because of his keen insight and natural intelligence that he came up with infinite series for π

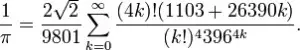
This series made up the basis of certain algorithms that are used today. One such remarkable instance is when he solved the bivariate problem of his roommate at spur of moment with a novel answer that solved the whole class of problems through continued fraction. Besides that he also led to draw some formerly unknown identities such as by linking coefficients of and providing identities for hyperbolic secant.

He also described in detail the mock theta function, a concept of mock modular form in mathematics. Initially, this concept remained an enigma but now it has been identified as holomorphic parts of maass forms. His numerous assertions in mathematics or concepts opened up new vistas of mathematical research for instance his conjecture of size of tau function that has distinct modular form in theory of modular forms. His papers became an inspiration with later mathematicians such as G. N. Watson, B. M. Wilson and Bruce Berndt to explore what Ramanujan discovered and to refine his work. His contribution towards development of mathematics particularly game theory remains unrivaled as it was based upon pure natural talent and enthusiasm. In recognition of his achievements, his birth date 22 December is celebrated in India as Mathematics Day. It would not be wrong to assume that he was first Indian mathematician who gained acknowledgment only because of his innate genius and talent.

His Publications

It was after his first publication in the “Journal of the Indian Mathematical Society” that he gained recognition as genius mathematician. With collaboration of English mathematician G. H. Hardy, with whom he came in contact with during his visit to England, he brought forward his divergent series that later stimulated research in that given area thus refining the contribution of Ramanujan. Both also worked on new asymptotic formula that gave rise to method of analytical number theory also called as “Circle Method” in mathematics.

It was during his visit to England that he got worldwide recognition after publication of his mathematical work in European journals. He also achieved the distinction of becoming second Indian, who was elected as Fellow of Royal Society of London in 1918.

Death

He died on 26 April 1920 at hands of dreadful disease of tuberculosis. Although he couldn’t get recognition of world at large but in field of mathematics, his contribution is duly recognized today.